Probably not what you think it does!
One of the most common requests that we get for calculated columns is for Mean Time Between Failure, or MTBF. This statistic seems to be embedded in the psyche of all biomedical engineers. How many of those, I wonder, actually know what it means? If someone asks for the MTBF of an individual asset that is a pretty sure sign that MTBF doesn’t mean what they think it means.
So you have a device with a published MTBF of 1,000,000 hours. Does that mean that if you have one of those devices then it is likely to run for 1,000,000 hours before it breaks? Of course not. It means that if you have 1,000,000 of those devices all running in identical situations, then the probability that one of the devices will fail within one hour is greater than 0.5 (i.e. more likely than not). Similarly, if you had 500,000 devices all running in identical situations, then it is more likely than not that one device will fail within two hours. You can do the maths for 2,000,000 devices (30 minutes until failure), or 250,000 devices (four hours before a likely failure). The first thing that it clear from this is that this metric is by no means an indicator for when (or how often) a device is likely to fail: simply change the number of devices on test and you change the probable time until a failure occurs.
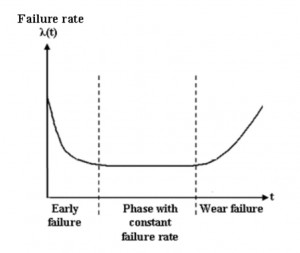
Another factor that you might not be aware of is that MTBF is only a meaningful metric for a very particular part of the life-cycle of a device. When a device is first delivered there is a relatively high probability of it failing soon after commissioning. This is because of problems inherent in the manufacturing process and is rather depressingly known as “infant mortality”. I personally prefer the term DOA (Dead on Arrival) which is equally morbid but doesn’t conjure up the same sad visual imagery. Also, as a device gets older, it will wear out and will fail more often. If you plot the failure rate of a device graphically you will see the famous “Bathtub Curve”.
No, not that bathtub curve! This one:
MTBF only has any meaning within the section of this curve where the failure rate is constant. If you’ve got maths O-Level you’ll know that means “the flat bit”. Ideally, the failure rate would be zero, but life’s not like that.
So, if you’re thinking of using MTBF as some kind of reliability metric, remember:
a. MTBF only has meaning over the entire life-cycle of the device. i.e. it doesn’t really mean anything until you’ve decommissioned all of them
b. MTBF for a single device is a meaningless concept
c. You should ignore the first N breakdowns and the last N breakdowns, where N is known only to your spirit guide
Quite a few people might need to read some or all of those point again, especially the second. A single device does not have a MTBF. You may as well ask for the square root of a negative number, the colour of the wind or the specific gravity of sadness. MTBF is a measure of probability, and probability as a mathematical concept only has meaning when the number of trials tends to infinity (1 is not even close to infinity!).
If you toss a coin an infinite number of times in identical circumstances, the probability of heads or tails is 1/2. If you toss a coin once, maths won’t help you. Probability is simply not defined mathematically for a sample size of 1. As the number of trials tends to infinity, so the number of heads and tails will tend towards equality. This is actually the definition of probability. If you think that after a long sequence of “heads”, nature steps in and causes a run of “tails”, then I’m afraid you don’t understand how probability works (this is known as the Gambler’s Fallacy) and I would invite you to a game of Russian Roulette. If played by an infinite number of Russians, then 1/6 of them would die and 5/6 would survive (although I’m not quite sure that I can get my head around what 1/6 of infinity actually means, especially as 1/6 of infinity = infinity, but now we are straying into number theory and countable infinity versus non-countable infinity). But, as you slowly raise the revolver to your temple and your trembling finger wraps around the trigger, I’m afraid that you are a single trial and maths won’t keep you alive. MTBF works the same way. The only thing that you can be sure of is that if an infinite number of Russians are involved the catering is likely to be abysmal and the queues very long.
So why does e-Quip include a built-in MTBF function?
There are a few arguments that I have come to accept that I will never win. One is that there is no need for VAT in a spare parts catalogue, and the other is MTBF. In my opinion, and in the opinion of a great many reliability engineers, MTBF is a meaningless concept unless you are considering an assembly of individual components, where the sum of the MTBF of the individual components gives an indication of the probable reliability of the assembly.
Despite my protestations and appeals to common sense, a great many people insist that the spare parts screen includes VAT. It is not my job to force my opinions onto the users of my software: if you want VAT on the spare parts screen, then VAT on the spare parts screen you shall have! I’m working with my analyst / priest at getting past this. MTBF is similar. Lots of people want it, even though I suspect that they are not entirely sure what it means.
On a recent trawl of the web (and you thought that my life was a thrilling, white-knuckle ride), I found this comment from a manufacturer:
“MTBF measurement is based on a statistical sample and is not intended to predict any one specific unit’s reliability; thus MTBF is not, and should not be construed as a warranty measurement.”
“I concur”, as they say in all good television medical dramas. There are lots of MTBF definitions. According to Wikipedia there are at least: MIL-HDBK-217F, Telcordia SR332, Siemens Norm, FIDES,UTE 80-810 (RDF2000), and probably a great many more. You pays your money and you takes your choice. Either way, e-Quip gives you the ability to calculate MTBF, just be sure that it really means what you think it means before you make any decisions based on it.